원문: 1998, Colm Mucahy and John Rossi, A Fresh Approach to the Singular Value Decomposition
선행개념: 행렬, 대각행렬, 전치행렬, 역행렬, 직교행렬, 고윳값, 고유벡터, 대각화, 직교대각화.
목차
- 소개
- 복소수의 극형식과 행렬의 극분해(Polar Decomposition)
- 특이값 분해(Singular Value Decomposition)
- 의사 역행렬(Pseudo-inverse)
- Solving All Systems
항이 실수인 행렬만 다루며, 여기서는 3의 주제를 다룬다.
연결된 포스팅 링크: 1부(주제1,2), 2부(주제3), 3부(주제4,5)
행렬의 극분해(Polar Decomposition) 예시
앞서서 가역인 행렬 $A$가 $A=RW$로 극분해 됨을 확인했다. $R$은 각 항이 양수인 대칭행렬, $W$는 직교행렬이다.
실제로 행렬 $ \begin{bmatrix} 1&1 \\ 0&1 \end{bmatrix} $ 의 $R, W$ 행렬을 구해보자.
$A A^{T}= \begin{bmatrix} 2&1 \\ 1&2 \end{bmatrix} $ 이므로 고윳값을 구하면
$ \begin{vmatrix} 2-\lambda &1 \\ 1&2 -\lambda \end{vmatrix} = 0 $
$ \lambda = \frac{1+\sqrt{5}}{\sqrt{2}}, \frac{1-\sqrt{5}}{\sqrt{2}}$
$ D = \begin{bmatrix} \frac{1+\sqrt{5}}{2} & 0 \\ 0 & \frac{1-\sqrt{5}}{\sqrt{2}} \end{bmatrix} $
$ P = \begin{bmatrix} \sqrt{\frac{5+\sqrt{5}}{10}} & \sqrt{\frac{5-\sqrt{5}}{10}} \\ \sqrt{\frac{5-\sqrt{5}}{10}} & -\sqrt{\frac{5+\sqrt{5}}{10}} \end{bmatrix} $
$R=PDP^{T}=\begin{bmatrix} \frac{3}{\sqrt{5}}&\frac{1}{\sqrt{5}} \\ -\frac{1}{\sqrt{5}}&\frac{2}{\sqrt{5}} \end{bmatrix}$
$W=R^{-1}A = \begin{bmatrix} \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \end{bmatrix}$
아래의 그림은 실제로 행렬 $W, R$ 순서로 선형변환한 그림이다.($A\mathbf{x}=RW\mathbf{x}$ 이므로 $W$부터 곱해진다.)
b그림에서 $W$ 선형변환을 살펴보면 $\cos \theta = \frac{2}{\sqrt{5}}, \, \sin \theta = \frac{1}{\sqrt{5}}$인 $\theta$각 만큼의 회전 변환임을 알 수 있다. c그림에서 $R$ 선형변환을 살펴보면 $D$의 고윳값들은 회전한 $x$축 방향으로 얼마만큼 늘리거나 줄였는지 나타내는 값으로 길이 변환임을 알 수 있다.
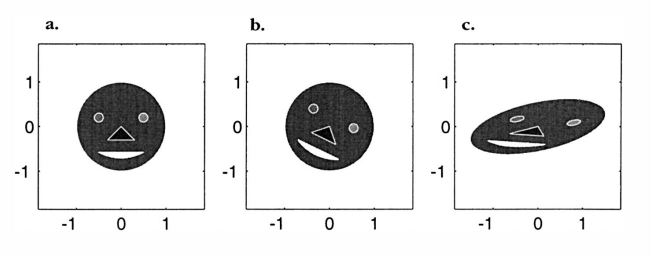
(출처: p202, A Fresh Approach to the Singular Value Decomposition(1998, Colm Mucahy and John Rossi)
3. 특이값 분해(Singular Value Decomposition)
극분해의 맹점은 가역행렬만 가능하다는 점이다. 또한 직교대각화는 대칭행렬만 가능하다는 문제가 있다.
하지만 실제 상황에서 만들어진 행렬은 이런 특성을 갖고 있지 않다.
이러한 문제를 해결할 수 있는 방법이 바로 특이값 분해(Singular Value Decomposition)이다.
$\mathbf{Theorem 2}$. 임의의 $m\times n$ 행렬 $A$에 대해
$m\times n$ 대각행렬 $D$, $n \times n$ 직교행렬 $U$, $ m \times m $ 직교행렬 $V$가 존재하여
$$A= U D V^{T}$$
로 표현이 가능하다.
또한 $rank(A)=r$ 일 때*, $AA^{T}$의 고윳값의 양의 제곱근을 차례로 $d_{1} \geq d_{2} \geq \cdots \geq d_{r}$라고 하면 이 값이 $D$의 대각선 항의 값이 된다. 이 고윳값에 차례로 대응되는 $A A^{T}$ 의 고유벡터를 열벡터로 하는 행렬이 $U$, $A^{T} A$의 고유벡터를 열벡터로 하는 행렬이 $V$가 된다.
이를 특이값 분해(Singular Value Decomposition)라고 한다.
$U= \begin{bmatrix}\vec{u_1} &\vec{u_2}&\cdots& \vec{u_r}\end{bmatrix} $
$V^T = \begin{bmatrix} \vec{v_1} \\ \vec{v_2} \\ \vdots \\ \vec{v_r} \end{bmatrix} $
$D = \begin{bmatrix}d_{1}&0&\cdots&0&\cdots\\0&d_{2}&\cdots&0&\cdots\\ \vdots&\vdots&\ddots&0&\cdots\\0&0&0&d_{r}&\cdots\\\vdots&\vdots&\vdots&\vdots&\ddots\end{bmatrix} $
$Proof$. (m=n인 가역행렬인 경우) 행렬의 극분해를 사용하여 $A=PDP^{T}W$라고 쓸 수 있으므로
$U=P, \, V'=P^{T} W$ 으로 두면 증명된다.
모든 경우에 대해 증명은 우리 수준을 넘어서므로 계산으로 간단히 확인해보자.
$AA^{T}, A^{T}A$는 $(AA^{T})^{T} = AA^{T} $으로 대칭행렬이므로 직교대각화가 가능하다.
SVD결과를 대입해 계산하면 $AA^{T}= U D^2 U^{T}, \; A^{T}A= V^{T} D^2 V$ 이므로
직교대각화 하여 표현한 형태임을 알 수 있고 $AA^{T}, A^{T}A$ 은 같은 양의 고윳값을 갖
$D$의 대각선의 원소를 고윳값에서 크기가 큰 순서로 나열하였으므로
$D$가 유일하게 결정되어 위와 같은 표현이 가능함을 확인할 수 있다.
* 계수(Rank)란 행렬의 독립인 열벡터의 갯수 또는 가우스 소거법으로 줄였을 때 0이 아닌 행의 갯수, 즉 행렬의 차원을 의미한다. 예를 들어 $ A= \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} $ 과 같은 행렬의 선형변환을 생각해보면 x축으로 정사영 시키는 변환이므로 차원이 1이다. 이를 기호로 표현하면 $rank(A)=1$ 이라고 할 수 있다.
예시를 통해 위의 결과를 확인해보자.
예1. 직교대각화와 SVD의 차이점
$ A= \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} $ 은 대칭행렬로 직교대각화가 가능하다. 직교대각화의 과정으로 고윳값을 계산하면 $3, -1$이고 SVD로 계산하면 $3, 1$이 나온다. 이것을 이용해 계산하면 아래와 같다. 차이점을 느껴보자.
직교대각화: $ A= \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} -1 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} ^T $
SVD: $ A= \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} ^T $
예2. 극분해와 SVD
$ A= \begin{bmatrix} 1&1 \\ 0&1 \end{bmatrix} $을 SVD로 계산하면 회전된 기저와 늘린 길이가 더 잘 보인다.
극분해: $A = \begin{bmatrix} \frac{3}{\sqrt{5}}&\frac{1}{\sqrt{5}} \\ -\frac{1}{\sqrt{5}}&\frac{2}{\sqrt{5}} \end{bmatrix} \begin{bmatrix} \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \end{bmatrix} $
SVD: $ A= \begin{bmatrix} \sqrt{\frac{5+\sqrt{5}}{10}} & \sqrt{\frac{5-\sqrt{5}}{10}} \\ \sqrt{\frac{5-\sqrt{5}}{10}} & -\sqrt{\frac{5+\sqrt{5}}{10}} \end{bmatrix} \begin{bmatrix} \frac{1+\sqrt{5}}{2} & 0 \\ 0 & \frac{1-\sqrt{5}}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \sqrt{\frac{5+\sqrt{5}}{10}} & -\sqrt{\frac{5-\sqrt{5}}{10}} \\ \sqrt{\frac{5-\sqrt{5}}{10}} & \sqrt{\frac{5+\sqrt{5}}{10}} \end{bmatrix}^{T} $
예3. 비가역행렬(역행렬이 존재하지 않는 행렬)의 SVD
$ A= \begin{bmatrix} -1&2 \\ 2&-4 \end{bmatrix} $ 는 $ad-bc=0$으로 역행렬이 존재하지 않는다. 따라서 극분해는 불가능하지만 SVD는 가능하다.
$A A^{T}, A^{T} A$에 대해 직교대각화하면
$ A A^{T} = A^{T} A = \begin{bmatrix} 5 & -10 \\ -10 & 20 \end{bmatrix}= \begin{bmatrix} -\frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \end{bmatrix} \begin{bmatrix} 25 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \frac{2}{\sqrt{5}} & -\frac{1}{\sqrt{5}} \\ -\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \end{bmatrix}^T$
따라서 SVD 결과는(위의 결과에 따라 앞의 P만을 취하면 된다.)
$ A = \begin{bmatrix} -\frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \end{bmatrix} \begin{bmatrix} 5 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} -\frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \end{bmatrix}^T$
한편 대칭행렬이므로 직교대각화가 가능하다. 직교대각화 하면
$ A = \begin{bmatrix} -\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \\ -\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \end{bmatrix} \begin{bmatrix} 0 & 0 \\ -5 & 0 \end{bmatrix} \begin{bmatrix} -\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \\ -\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \end{bmatrix}^T$
예4. 정사각행렬이 아니어서 비가역이고 직교대각화도 불가능한 경우
$A = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$
$ A A^{T} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix}^T $
$ A^{T} A = \begin{bmatrix} 1 \end{bmatrix} = \begin{bmatrix} 1 \end{bmatrix} \begin{bmatrix} 1 \end{bmatrix} \begin{bmatrix} 1 \end{bmatrix}^T $
따라서 SVD 결과는 $A = \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \sqrt{2} \\ 0 \end{bmatrix} \begin{bmatrix} 1 \end{bmatrix}^T $
다음 시간에는 의사역행렬(Pseudo-inverse)에 대해서 알아보자.
'수학 > 수학 논문 정리' 카테고리의 다른 글
| Quaternion으로 $\mathbb{E}^3$ 공간에서 회전 예시 (0) | 2020.11.15 |
|---|---|
| A Fresh Approach to the Singular Value Decomposition 마지막 (0) | 2020.11.12 |
| A Fresh Approach to the Singular Value Decomposition 첫 번째 (0) | 2020.11.11 |
| Quaternions and Rotations in $\mathbb{E}^4$ 두 번째 (0) | 2020.11.08 |
| Quaternions and Rotations in $\mathbb{E}^4$ 첫 번째 (2) | 2020.11.08 |

