원문: 2005, Joel L. Weiner and George.R Wilkens, Quaternions and Rotations in $\mathbb{E}^4$
필요한 개념: 벡터공간, 내적, 외적, 오일러 공식, 선형변환.
(환(ring), 벡터 공간의 합, 불변부분공간, 직교여공간은 사용될 때에 주석으로 간단하게 설명)
논문의 순서는 다음과 같다. 여기서는 3번의 주제를 다룬다. 4,5는 추후 다룰 예정.
- Introduction
- 내적(inner product)을 포함한 사원수환(Quaternion algebra) $\mathbb{H}$의 성질 정리
- 단위사원수(unit Quaternion) $\mathbf{p,q}$로 회전변환 $\boldsymbol{C}_\mathbf{p,q} : \mathbb{H} \longrightarrow \mathbb{H} $ 정의 및 3차원 공간에서의 회전변환 성질 정리
- 상미분방정식에서의 활용
- $\mathbb{E}^4$의 직교변환에서 변하지 않는 2차원 불변부분공간(2-dimensional subspace) 찾기
실제 사용하는 법 링크: 예시
들어가기 전에 오일러 회전의 문제점부터 짚고 가자.
짐벌 락(gimbal lock) 현상이란?
(이미지: By Drummyfish - Own work, CC0, 위키백과)
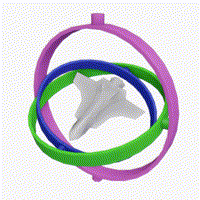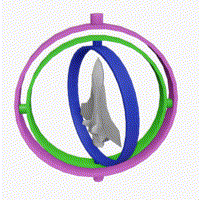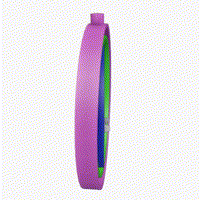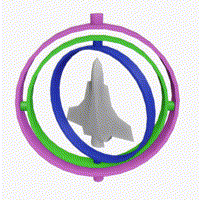
회전한다고 하면 흔히 $x, y, z$축 기준으로 회전하는 것을 생각할 것이다.
이 때 회전축을 짐벌이라고 한다.
문제는 회전하다보면 회전축 자체도 같이 회전하므로 회전축끼리 일치하게 되어
이를 풀어주지 않으면 원하는 회전을 못 시키게 된다는 것이다. (위 이미지 참고)
따라서 회전축끼리 묶이는 짐벌락 현상이 일어나면 회전할 때 최단거리로 움직이지 않고 이상한 모양으로 움직인다.
이 문제는 3D 그래픽 디자인 뿐만 아니라 항공기 등을 운항할 때 큰 문제가 될 수 있다.
이를 해결하려면 짐벌에 의존하지 않는 회전을 해야한다. 이를 위해선 3차원에 고정된 축이 아닌 새로운 축을 잡기 위해
차원을 하나 높일 필요가 있으며, 가장 적합한 것이 사원수를 활용한 회전이다.
$\mathbb{R}$-선형변환*: $\mathbb{H}$ 에서의 왼쪽 및 오른쪽 곱으로 정의된 함수
$\mathbf{q}$를 사원수라 하자. 그러면 두 선형변환 함수 $L_{\mathbf{q}}: \mathbb{H} \longrightarrow \mathbb{H},\; R_{\mathbf{q}}: \mathbb{H} \longrightarrow \mathbb{H}$를 다음과 같이 정의할 수 있다.
$$L_{\mathbf{q}}(\mathbf{x})=\mathbf{qx},\; R_{\mathbf{q}}(\mathbf{x})=\mathbf{xq}$$
$\mathbf{q}$를 단위사원수라고 하면 $L_{\mathbf{q}}, R_{\mathbf{q}}$는 $\mathbb{H}$ 직교 변환(orthogonal transformation)임을 알 수 있다. 이 사실이 왜 중요하냐면 직교 변환은 내적을 보존하는 변환이기 때문이다. 내적을 보존하는 변환은 길이와 각도를 보존하므로 회전변환이 이와 관련이 있다. 이를 다음의 식을 통해 간단히 보일 수 있다.(이전 포스트에서 보였던 식을 기억하자.)
$$|L_{\mathbf{q}}(\mathbf{x})|=|\mathbf{qx}|= |\mathbf{q}||\mathbf{x}|=|\mathbf{x}|$$
단위 사원수 $\mathbf{p}$, $\mathbf{q}$에 대해 함수(mapping) $C_{\mathbf{p,q}}:\mathbb{H} \longrightarrow \mathbb{H}$를 아래와 같이 함수의 합성으로 정의하면, 순서를 바꿔 합성해도 같으며 직교 변환임을 쉽게 알 수 있다.
$$C_{\mathbf{p,q}}=L_{\mathbf{p}} \circ R_{\mathbf{q}}=R_{\mathbf{q}} \circ L_{\mathbf{p}}$$
5번째 주제에서 사용하게 될 간단한 공식이다. 성립은 함수식에 대입해보면 간단히 보일 수 있다.
$$C_{\mathbf{p_1,q_1}} \circ C_{\mathbf{p_2,q_2}}= C_{\mathbf{p_1 p_2,q_1 q_2}}$$
*선형변환은 덧셈, 상수배 연산을 유지하는 함수이다.
$\mathbb{E}^3$에서의 사원수(Quaternion)를 이용한 회전변환
이제 본격적으로 단위사원수 $\mathbf{q}$에 대한 선형변환 $C_{\mathbf{q},\overline{\mathbf{q}}}$ 에 대해서 살펴보자. 이것을 간단하게 $C$라고 할 것이다.
앞서서 정리했듯 순단위사원수$\mathbf{u}$에 대해 $\mathbf{q}=e^{\mathbf{u}\theta}$ 라고 쓸 수 있다. 그러면
$$C(\mathbf{x})=\mathbf{qx\overline{q}}=e^{\mathbf{u}\theta}\mathbf{x}e^{-\mathbf{u}\theta}$$
이다. $C(\mathbf{1})=\mathbf{q1\overline{q}}=\mathbf{q\overline{q}1}=1\mathbf{1}=\mathbf{1}$ 이므로 스칼라 사원수인 $\mathbf{1}$은 보존하는 것을 알 수 있다. 즉 $\mathbb{E}^3$에 대응되는 순사원수($q_0=0$인 사원수)만 직교변환되므로 선형변환 $C$를 $\mathbb{E}^3$에 국한된 선형변환이라고 할 수 있다. $\mathbf{u}=\vec{u} \in \mathbb{E}^3$임을 주목하자.
드디어 회전변환에 대한 정리는 다음과 같다.
$\mathbf{Proposition 1.}$ 만약 $\mathbf{q}$이 단위사원수라면, 순단위사원수 $\mathbf{u}$와 실수 스칼라 $\theta$가 존재하여 $\mathbf{q}=e^{\mathbf{u}\theta}$이며, $C(\mathbf{x})=\mathbf{qx\overline{q}}$으로 정의된 선형변환 $C:\mathbb{E}^3 \longrightarrow \mathbb{E}^3$ 은 $\mathbf{u}$에 수직인 평면을 기준으로 $2\theta$ 만큼 회전하는 변환이다.
$Proof.$ 앞의 포스팅에서 $\mathbf{q}=e^{\mathbf{u}\theta}$임은 오일러 공식으로 간단하게 이미 보였다.
$$\frac{d}{d\theta}e^{\mathbf{u}\theta} = -\mathbf{1}\sin \theta +\mathbf{u}\cos \theta = \mathbf{u}e^{\mathbf{u}\theta} = e^{\mathbf{u}\theta}\mathbf{u}$$
이므로 $ \mathbf{u} = \vec{u} $ 은 $e^{\mathbf{u} \theta}$ 와 곱셈에서 교환가능하다.(사원수 곱은 교환법칙이 안된다.)
이를 통해 $C(\vec{u})=e^{\mathbf{u}\theta} \mathbf{u} e^{-\mathbf{u}\theta}= \vec{u}$ 임을 관찰할 수 있다.
그러므로 $C$는 $\mathbf{u}=\vec{u}$으로 생성(span)되는 부분공간(subspace)** $L$을 고정하고 움직이는 변환을 알 수 있다.
쉽게 말하면 $\vec{u}$를 방향벡터로 하고 원점을 지나는 직선 $L$은 선형변환 $C$에 의해 변하지 않으므로 축의 역할임을 알 수 있다.
(선형변환에서 배운 eigenvector와 유사한 역할을 하고 있다.여기서는 심지어 길이도 변하지 않는다.)
그러므로 직교여공간***(orthogonal complement)인 $L^{\bot} \subset \mathbb{E}^3$ 또한 잘 정의된다.
$\mathbf{v}=\vec{v}$를 $L^{\bot}$ 위의 단위벡터(순단위사원수)라고 하고, $\mathbf{w}=\mathbf{uv}=\vec{u}\times\vec{v}$라고 하자. (사원수 곱임을 기억하자)
또한, 앞의 포스팅에서 $\mathbf{u,v}$은 서로 수직인 순단위사원수이므로 $\mathbf{uv}=-\mathbf{vu}$ 임을 보였다.
따라서 등식 $\mathbf{v}e^{-\mathbf{u}\theta}=e^{\mathbf{u}\theta}\mathbf{v}$ 을 만족시킨다.
($e^{\mathbf{u}\theta}=\mathbf{1}\cos \theta +\mathbf{u}\sin \theta$을 대입해보면 알 수 있다.)
그러므로,
$$ \begin{split} C(\vec{v}) &= e^{\mathbf{u}\theta} \mathbf{v} e^{-\mathbf{u}\theta} \ &= e^{2 \mathbf{u}\theta}\mathbf{v} \ &= \cos(2\theta)\vec{v} + \sin (2 \theta) \vec{w} \end{split} $$
이다.
다시 말해 이것은 $\mathbf{u}$을 축으로 하고 $\mathbf{u}$와 수직인 $L^{\bot}$ 공간(서로 수직인 $\vec{v}, \vec{w}$ 벡터를 기저로 갖는 공간) 을 $2\theta$만큼 회전시킨 변환임을 알 수 있다.

**부분공간은 벡터 공간의 부분집합으로 벡터의 합, 스칼라배를 했을 때 다시 그 부분공간에 존재하면 (연산에 대해 닫혀있는 경우) 부분공간이라고 한다. 예를 들면 평면 벡터공간의 부분공간에는 직선이 있다. 직선 위의 어떤 벡터를 더하거나 실수배하든지 다시 직선 위의 점이 되기 때문이다.
***어떤 부분공간의 수직인 벡터들로 이루어진 부분공간을 의미한다. 예를 들면 직선의 직교여공간은 그 직선의 방향벡터를 법선벡터로 하는 평면이 된다.
'수학 > 수학 논문 정리' 카테고리의 다른 글
| Quaternion으로 $\mathbb{E}^3$ 공간에서 회전 예시 (0) | 2020.11.15 |
|---|---|
| A Fresh Approach to the Singular Value Decomposition 마지막 (0) | 2020.11.12 |
| A Fresh Approach to the Singular Value Decomposition 두 번째 (0) | 2020.11.11 |
| A Fresh Approach to the Singular Value Decomposition 첫 번째 (0) | 2020.11.11 |
| Quaternions and Rotations in $\mathbb{E}^4$ 첫 번째 (2) | 2020.11.08 |
